Betonzuschlagstoffe sind körnige Agglomerate, deshalb sind neben Gesteinszusammensetzung und -zustand, ihre wichtigsten Eigenschaften die Korngrößenverteilung, die Kornform und die Kornrauhigkeit, die unter dem Sammelnamen Granulometrie entsprechend den Anwendungsgebieten durch Zusatz der Stein- und Kiesindustrie verändert werden kann. Um dies bestimmen zu können, benötigen wir eine einheitliche Methode zur Beschreibung der Granulometrie und die Kenntnis, was diese Kennwerte betontechnologisch bedeuten.

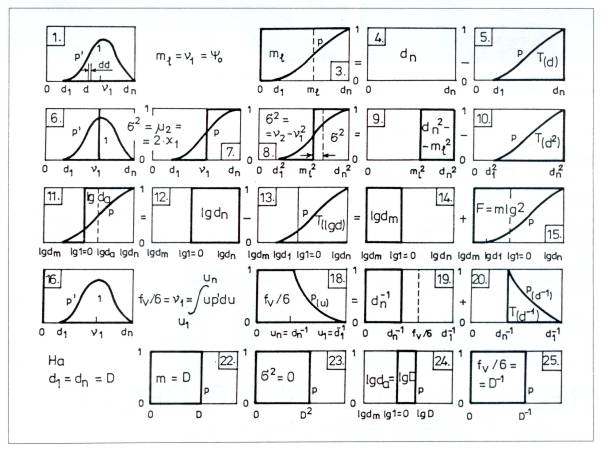
Abbildung 1.: Die Graphoanalytik der Kornverteilungskennwerte

Eine bedeutende Rolle unter all diesen Werten kommt der durchschnittlichen Korngröße d_n zu, die im Gegensatz zum Feinheitsmodul vom Abszissenanfangswert d_m unabhängig ist. Solange sie zwichen dem Feinheitsmodul und der spezifichen volumetrischen Oberfläche liegt, gibt es zwischen der letzteren und dem Hohlraumgehalt keine Trendverbindung. Grund dafür ist, daß der Hohlraumgehalt zum Kornaggregat gehört, und im Gegensatz zum Feinheitsmodul und zur spezifichen volumetrischen Oberfläche, im Falle eines Einzelkornes keinen auslegbaren Begriff darstellt. Der Hohlraumgehalt, ebenalls im Gegensatz zu den zwei obigen granulometrischen Kennwerten, kann nicht durch die Superposition der eigenen ähnlichen Eigenschaften der Einzelkörner dargestellt werden, sondern wird durch das gegenseitige Größenverhältnis der Körner des Aggregats und durch die Art der Verdichtung bestimmt. Der Hohlraumgehalt des Aggregats mit harmonisch veränderlicher Granulometrie ist mit guter Näherung die Größe, die dem Quotienten der Aggregatgrenzen proportional und von den anderen granulometrischen Kennwerten ebenfalls unabhängig ist (Abbildung 2.).

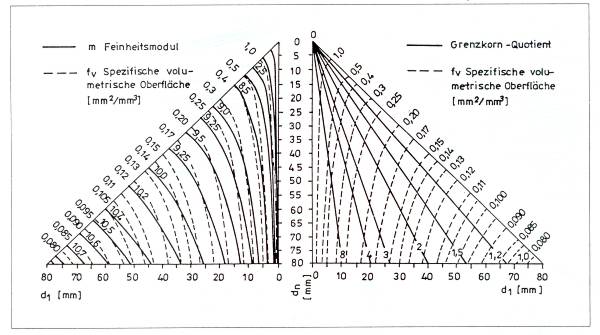
Abbildung 2.: Die Isokurven der Kornverteilungskennwerte

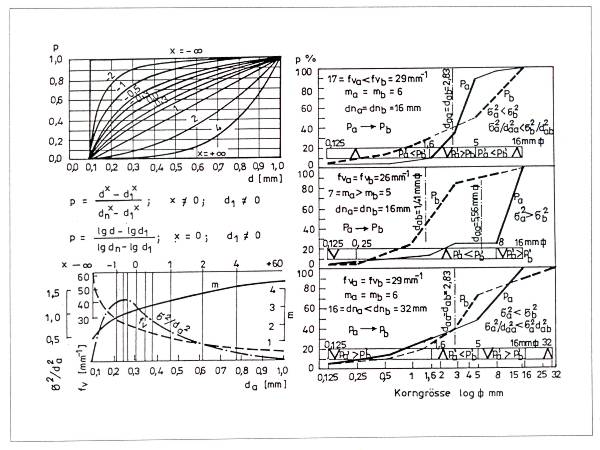
Abbildung 3.: Die Änderung des relativen Streuungsquadrates

Die Konsistenz des Betons, wie auch seine Druckfestigkeit, lassen sich auch als Funktion des Feinheitsmoduls und der spezifischen volumetrischen Oberfläche ausdrücken, und dieser Zusammenhang wird auch vom Wasser-Zement-Wert, von der Güte und Menge des Zementes beeinflußt. Wird die Konsistenzfunktion in der Form einer windschiefen Fläche geschrieben, so bilden ihre Deklinationskurven eine in der Ebene parallel laufende Geradenreihe und bestätigen, daß dis Konsistenz vor allem von der spezifischen volumetrischen Oberfläche beeinflußt wird, während die Änderungswirkung des Feinheitsmoduls geringer ist. Die Funktion der Druckfestigkeit haben wir in der Form einer Paraboloidfläche ausgedrückt, deren Planschnitte verschiedene Kegellinien ergeben. Demnach hat die Druckfestigkeitsfunktion ein Maximum, während ihre unabhängigen Veränderlichen ein Optimum haben, was sich in einer größeren spezifischen volumetrischen Oberflöche bemerkbar macht als auf Grund der Fuller-Kurve zu erwarten wäre. Die Abweichung vom Optimum kann sogar einen 50 %igen Verlust der Druckfestigkeit verursachen, dessen Vermeidung einen schwerwiegenden Grund für die Notwendigkeit einer Zwei-Parameter-Kennzeichnung der Granulometrie bildet. Der schon erwrähnte Trendzusammenhang zwischen der spezifischen volumetrischen Oberfläche und dem Feinheitsmodul ermöglicht gleichzeitig, daß die zur Erreichung der geplanten Betondruckfestigkeit notwendige Zementzugabe - nebst gegebener Konsistenz, Zementquatität und Wasser-Zement-Wert - in der Funktion des Feinheitsmoduls angageben werden soll (Abbildung 4.).

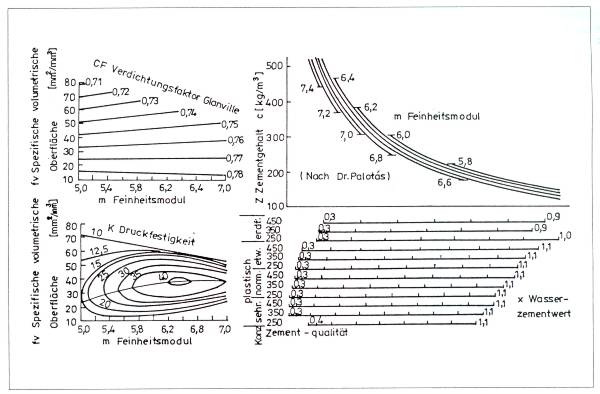
Abbildung 4.: Nomogramme zur Mischungsverhältnisbestimmung des Betons

Wünscht man den Zuschlag aus drei Fraktionen herzustellen, so ist die Berechnung der Proportionalität der Fraktionen eine Aufgabe mit drei Unbekannten, deren graphoanalytische Lösung bei Zwei-Parameter-Kennzeichnung der Kornverteilung eindeutig ist. Die zwei Kennwerte der Kornverteilung sind vorzugsweise der Feinheitsmodul und die spezifische volumetrische Oberfleche, in deren Koordinatensystem die Kornaggregate durch ihre Darstellungspunkte besimmt sind. Zur graphoanalytischen Lösung der Aufgabe kann eine statische Analogie angawendet werden: eine Ersatzkraft von bekannter Größe und Wirkungslinie soll in drei parallele räumliche Kräfte mit bekannten Wirkungslinien zerlegt werden, ader aber - was das selbe ist - man erhält den Anteil einer Fraktion, wenn man den Quotienten, der aus dem Darstellungspunkt des Zuschlages und der Fraktion auf die zur letzteren gegenüberliegenden Dreieckseite geführten senkrechten Entfernungen ermittelt, oder wenn man das Flächenverhältnis des zu den erwähnten Darstellungspunkten gehörigen Dreiecks aufstellt. Die Berechnung der Fraktionsanteile kann auch zu Sonderfällen, so z.B. zu einer Dreieckabbildungsaufgabe oder zu einem statischen Planarproblem mit zwei Unbekannten entzerrt werden. Nach letzterem soll der statischen Analogie gemäß die Ersatzkraft von bekannter Größe und Wirkungslinie in zwei parallele ebene Kräfte mit bekannten Wirkungslinien zerlegt werden. Die Lösung ist durch die Seileckkonstruktion gegeben. Diese Methode kann angewendet werden, wenn der Zuschlag und seine zwei Fraktionen mit einem einzigen Parameter, z.B. mit dem Feinheitsmodul, gekennzeichnet werden. Zurückkommend auf die Zusammensetzung des Dreifraktionenzuschlages kann die Größe der Fraktionsanteile auch durch den Minimalbetrag des Fehlerquadrats der geplanten und der effektiven granulometrischen Kurven, d.h. durch dia Regressionsberechnung der Granulometrie bestimmt werden (Abbildung 5.).

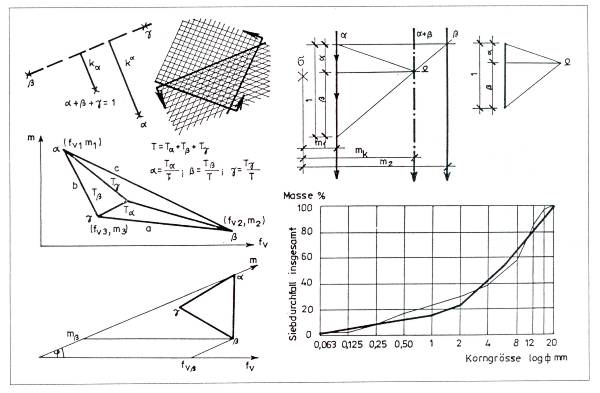
Abbildung 5.: Kornverteilungsbestimmug mittels Graphoanalytik

Die Abweichungen dar Form, des Volumens und der spezifischen Oberfläche von Zuschlagstoffen, die aus gedrungenen oder flachen Körnern bestehen, können in einem Koordinatensystem, das die Achsenverhältnisse enthält, dargestellt werden. Im Falle von Splitten ist die gedrungene Kornform für die Druckfestigkeit, den Zementanspruch und die Verarbeitbarkeit, die flache Kornforrn wieder für die Biegezugfestigkeit des Betons vorteilhaft. Bei Anwendung von Splitten steigt auch die Drucktestigkeit und die Reißzugtestigkeit im Verhältnis zu jenen des aus natürlichem Rundkies hergestellten Betons (Abbildung 6.).

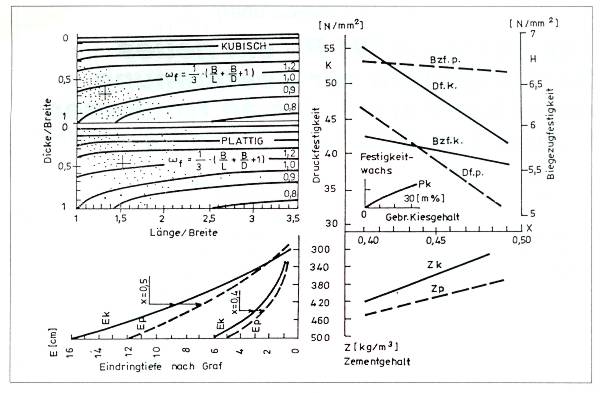
Abbildung 6.: Kennzeichnung und Betontechnologie der Kornform